Rayleigh quotient minimization for absolutely one-homogeneous functionals
Résumé
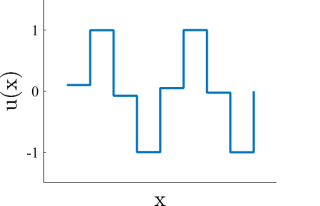
In this paper we examine the problem of minimizing generalized Rayleigh quotients of the form J(u)/H(u), where both J and H are absolutely one-homogeneous functionals. This can be viewed as minimizing J where the solution is constrained to be on a generalized sphere with H(u) = 1, where H is any norm or semi-norm. The solution admits a nonlinear eigenvalue problem, based on the subgradients of J and H. We examine several flows which minimize the ratio. This is done both by time-continuous flow formulations and by discrete iterations. We focus on a certain flow, which is easier to analyze theoretically, following the theory of Brezis on flows with maximal monotone operators. A comprehensive theory is established, including convergence of the flow. We then turn into a more specific case of minimizing graph total variation on the L1 sphere, which approximates the Cheeger-cut problem. Experimental results show the applicability of such algorithms for clustering and classification of images.
Domaines
Traitement des images [eess.IV]
Fichier principal
 hal-rayleigh.pdf (514.8 Ko)
Télécharger le fichier
hal-rayleigh.pdf (514.8 Ko)
Télécharger le fichier
 Flow_limit_u.png (6.28 Ko)
Télécharger le fichier
Flow_limit_u.png (6.28 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...