Overrelaxed Sinkhorn-Knopp Algorithm for Regularized Optimal Transport
Résumé
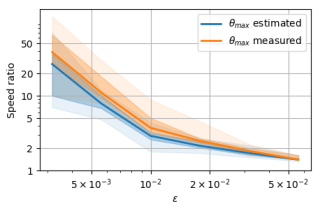
This article describes a method for quickly computing the solution to the regularized optimal transport problem. It generalizes and improves upon the widely-used iterative Bregman projections algorithm (or Sinkhorn-Knopp algorithm). The idea is to overrelax the Bregman projection operators, allowing for faster convergence. In practice this corresponds to elevating the diagonal scaling factors to a given power, at each step of the algorithm. We propose a simple method for establishing global convergence by ensuring the decrease of a Lyapunov function at each step. An adaptive choice of overrelaxation parameter based on the Lyapunov function is constructed. We also suggest a heuristic to choose a suitable asymptotic overrelaxation parameter, based on a local convergence analysis. Our numerical experiments show a gain in convergence speed by an order of magnitude in certain regimes.
Fichier principal
 hal.pdf (309.75 Ko)
Télécharger le fichier
hal.pdf (309.75 Ko)
Télécharger le fichier
 speedratio_ML.png (37.58 Ko)
Télécharger le fichier
speedratio_ML.png (37.58 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Loading...