Non-smooth modal analysis of piecewise-linear impact oscillators

Anders Thorin (1) , Pierre Delezoide (2) , Mathias Legrand (1)

1 Structural Dynamics and Vibration Laboratory [Montréal]
2 Chercheur indépendant

Periodic solutions of autonomous and conservative second-order dynamical systems of finite dimension n undergoing one unilateral contact condition are investigated in continuous time. The unilateral constraint is complemented with a purely elastic impact law which preserves total energy. The dynamics is linear when there is no contact. The number $k$ of impacts per period arises as a natural parameter of the proposed formulation. Interestingly, the existence of the targeted periodic solutions is essentially governed by a system of only $k-1$ nonlinear equations with k unknowns, regardless of the number of degrees-of-freedom. This serves to prove that the phase-space is populated by one-dimensional continua of periodic solutions generating invariant manifolds which can be understood as nonsmooth modes of vibration in the context of vibration analysis. Additionally, these equations provide an efficient and systematic way of calculating nonsmooth modes of vibration. They also demonstrate the existence of interesting properties: symmetries of trajectories and emergence of unique features such as manifolds supporting constant-frequency orbits. All results are illustrated through a simple in-line spring–mass system whose last mass undergoes the unilateral impact law. Stability is briefly discussed and a few neutrally stable modes are depicted.

• Animation corresponding to Fig. 7 (top left):
  
• Animation corresponding to Fig. 10 (top left):
  
• Animation corresponding to Fig. 15 (top left):
  
• Example of a stable motion with 3 impacts per period (gray: nonsmooth mode, blue: with perturbation):
  
• 20-dof, 1 impact per period:
  
• 20-dof, 5 impacts per period:
  
• 50-dof, 1 impact per period:
  
• 50-dof, 5 impacts per period:
  
• Finite Element model with a non-diagonal mass matrix, 1 ipp:
  
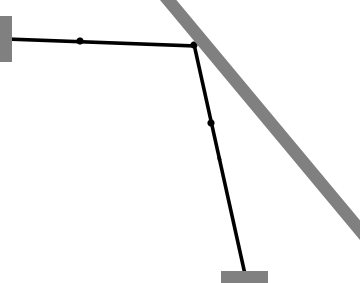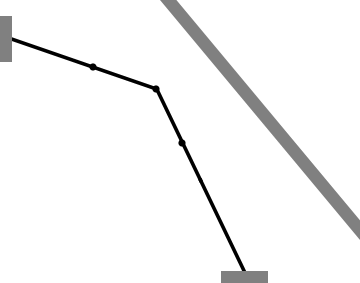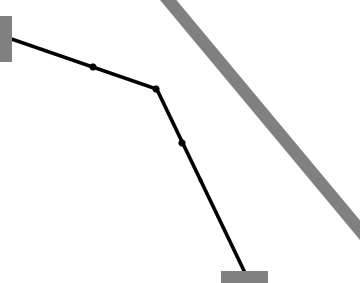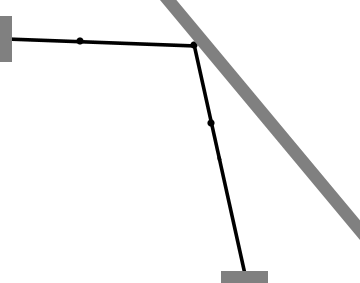
• Finite Element model with a non-diagonal mass matrix, 2 ipp:
  
• Finite Element model with a non-diagonal mass matrix, 5 ipp:
  

Mots clés: modal analysis; non-linear modal analysis; impact oscillators; non-smooth modes; nonlinear normal modes

Mots clés: modes non-réguliers; oscillateurs à impacts; analyse modale; analyse modale non-linéaire

Domaines: Vibrations [physics.class-ph]; Dynamique, vibrations

Anders Thorin, Pierre Delezoide, Mathias Legrand. Non-smooth modal analysis of piecewise-linear impact oscillators. SIAM Journal on Applied Dynamical Systems, 2017, 16 (3), pp.1710-1747. ⟨10.1137/16M1081506⟩. ⟨hal-01298983v2⟩