Computing Smooth Surface Contours with Accurate Topology
Résumé
This paper introduces a method for accurately computing the visible contours of a smooth 3D surface for stylization. This is a surprisingly difficult problem, and previous methods are prone to topological errors, such as gaps in the outline. Our approach is to generate, for each viewpoint, a new triangle mesh with contours that are topologically-equivalent and geometrically close to those of the original smooth surface. The contours of the mesh can then be rendered with exact visibility. The core of the approach is Contour-Consistency, a way to prove topological equivalence between the contours of two surfaces. Producing a surface tessellation that satisfies this property is itself challenging; to this end, we introduce a type of triangle that ensures consistency at the contour. We then introduce an iterative mesh generation procedure, based on these ideas. This procedure does not fully guarantee consistency, but errors are not noticeable in our experiments. Our algorithm can operate on any smooth input surface representation; we use Catmull-Clark subdivision surfaces in our implementation. We demonstrate results computing contours of complex 3D objects, on which our method eliminates the contour artifacts of other methods.
Fichier principal
 contours.pdf (5.75 Mo)
Télécharger le fichier
contours.pdf (5.75 Mo)
Télécharger le fichier
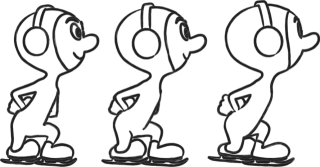 sanjay2_opt.png (156.38 Ko)
Télécharger le fichier
sanjay2_opt.png (156.38 Ko)
Télécharger le fichier
 Sanjay2_toon_opt.png (1005.82 Ko)
Télécharger le fichier
Sanjay2_toon_opt.png (1005.82 Ko)
Télécharger le fichier
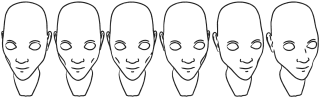 angela_DT.png (229.83 Ko)
Télécharger le fichier
contours.flv (23.66 Mo)
Télécharger le fichier
contours.mov (99.62 Mo)
Télécharger le fichier
angela_DT.png (229.83 Ko)
Télécharger le fichier
contours.flv (23.66 Mo)
Télécharger le fichier
contours.mov (99.62 Mo)
Télécharger le fichier
 walk_texture-candle_DT.png (281.56 Ko)
Télécharger le fichier
walk_texture-candle_DT.png (281.56 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Vidéo
Format : Vidéo
Format : Figure, Image
Loading...