Topology Preserving Simplification of 2D Non-Manifold Meshes with Embedded Structures
Résumé
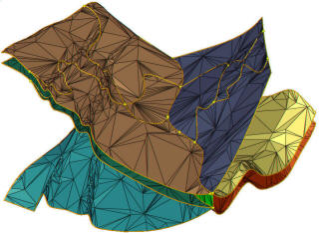
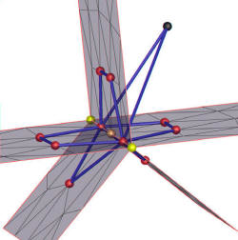
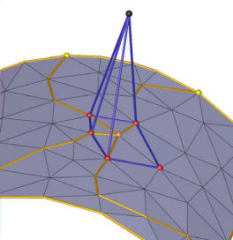
Mesh simplification has received tremendous attention over the past years. Most of the previous works deal with a proper choice of error measures to guide the simplification. Preserving the topological characteristics of the mesh and possibly of data attached to the mesh is a more recent topic, the present paper is about.We introduce a new topology preserving simplification algorithm for triangular meshes, possibly non-manifold, with embedded polylines. In this context embedded means that the edges of the polylines are also edges of the mesh. The paper introduces a robust test to detect if the collapse of an edge in the mesh modifies either the topology of the mesh or the topology of the embedded polylines. This validity test is derived using combinatorial topology results. More precisely we define a so-called extended complex from the input mesh and the embedded polylines. We show that if an edge collapse of the mesh preserves the topology of this extended complex, then it also preserves both the topology of the mesh and the embedded polylines. Our validity test can be used for any 2-complex mesh, including non-manifold triangular meshes. It can be combined with any previously introduced error measure. Implementation of this validity test is described. We demonstrate the power and versatility of our method with scientific data sets from neuroscience, geology and CAD/CAM models from mechanical engineering.
Fichier principal
 pg05.pdf (6.1 Mo)
Télécharger le fichier
pg05.pdf (6.1 Mo)
Télécharger le fichier
 AbstraPG05_1.jpg (22.27 Ko)
Télécharger le fichier
AbstraPG05_1.jpg (22.27 Ko)
Télécharger le fichier
 AbstraPG05_2.jpg (21.1 Ko)
Télécharger le fichier
AbstraPG05_2.jpg (21.1 Ko)
Télécharger le fichier
 AbstraPG05_3.jpg (11.71 Ko)
Télécharger le fichier
AbstraPG05_3.jpg (11.71 Ko)
Télécharger le fichier
 AbstraPG05_4.jpg (12.8 Ko)
Télécharger le fichier
AbstraPG05_4.jpg (12.8 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Loading...