Hierarchical Triangular Splines
Résumé
Smooth parametric surfaces interpolating triangular meshes are very useful for modeling surfaces of arbitrary topology. Several interpolants based on this kind of surfaces have been developed over the last fifteen years. However, with current 3D acquisition equipments, models are becoming more and more complex. Since previous interpolating methods lack a local refinement property, there is no way to locally adapt the level of detail. In this paper, we introduce a hierarchical triangular surface model. The surface is overall tangent plane continuous and is defined parametrically as a piecewise quintic polynomial. It can be adaptively refined while preserving the overall tangent plane continuity. This model enables designers to create a complex smooth surface composed of a small number of patches, to which details can be added by locally refining the patches until an arbitrary small size is reached. It is implemented as a hierarchical data structure where the top layer describes a coarse, smooth base surface, and the lower levels encode the details in local frame coordinates.
Fichier principal
 YHB05-TOG.pdf (2.42 Mo)
Télécharger le fichier
YHB05-TOG.pdf (2.42 Mo)
Télécharger le fichier
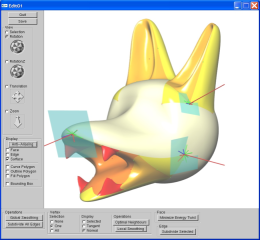 AAA.jpg (154.07 Ko)
Télécharger le fichier
AAA.jpg (154.07 Ko)
Télécharger le fichier
 f12a.jpg (23.61 Ko)
Télécharger le fichier
f12a.jpg (23.61 Ko)
Télécharger le fichier
 f12b.jpg (30.16 Ko)
Télécharger le fichier
f12b.jpg (30.16 Ko)
Télécharger le fichier
 f12c.jpg (51.19 Ko)
Télécharger le fichier
f12c.jpg (51.19 Ko)
Télécharger le fichier
 f12d.jpg (36.64 Ko)
Télécharger le fichier
f12d.jpg (36.64 Ko)
Télécharger le fichier
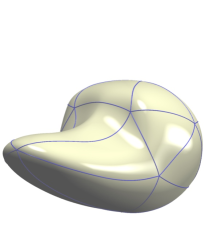 f12e.jpg (47.01 Ko)
Télécharger le fichier
f12e.jpg (47.01 Ko)
Télécharger le fichier
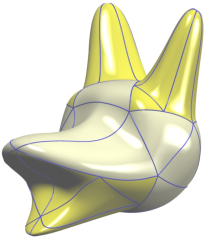 f12f.jpg (79.32 Ko)
Télécharger le fichier
f12f.jpg (79.32 Ko)
Télécharger le fichier
 f12g.jpg (58.32 Ko)
Télécharger le fichier
f12g.jpg (58.32 Ko)
Télécharger le fichier
 f12h.jpg (58.87 Ko)
Télécharger le fichier
f12h.jpg (58.87 Ko)
Télécharger le fichier
 f12i.jpg (61.16 Ko)
Télécharger le fichier
f12i.jpg (61.16 Ko)
Télécharger le fichier
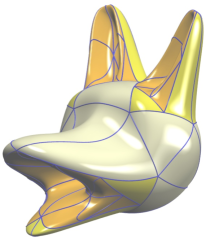 f12j.jpg (88.48 Ko)
Télécharger le fichier
f12j.jpg (88.48 Ko)
Télécharger le fichier
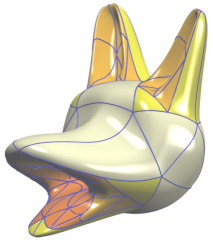 f12k.jpg (92.11 Ko)
Télécharger le fichier
f12k.jpg (92.11 Ko)
Télécharger le fichier
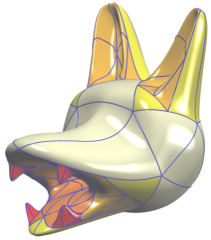 f12l.jpg (94.22 Ko)
Télécharger le fichier
f12l.jpg (94.22 Ko)
Télécharger le fichier
 fig_sect5_a.jpg (107.94 Ko)
Télécharger le fichier
fig_sect5_a.jpg (107.94 Ko)
Télécharger le fichier
 fig_sect5_b.jpg (96.5 Ko)
Télécharger le fichier
fig_sect5_b.jpg (96.5 Ko)
Télécharger le fichier
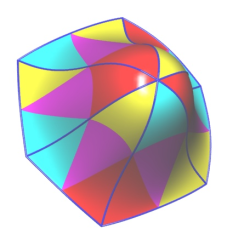 fig_sect5_c.jpg (41.75 Ko)
Télécharger le fichier
fig_sect5_c.jpg (41.75 Ko)
Télécharger le fichier
 fig_sect5_d.jpg (123.4 Ko)
Télécharger le fichier
fig_sect5_d.jpg (123.4 Ko)
Télécharger le fichier
 flying1.jpg (19.95 Ko)
Télécharger le fichier
flying1.jpg (19.95 Ko)
Télécharger le fichier
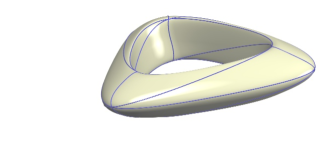 flying1c.jpg (32.14 Ko)
Télécharger le fichier
flying1c.jpg (32.14 Ko)
Télécharger le fichier
 flying2.jpg (22.55 Ko)
Télécharger le fichier
flying2.jpg (22.55 Ko)
Télécharger le fichier
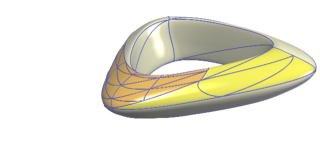 flying2c.jpg (39.92 Ko)
Télécharger le fichier
flying2c.jpg (39.92 Ko)
Télécharger le fichier
 flying3.jpg (23.87 Ko)
Télécharger le fichier
flying3.jpg (23.87 Ko)
Télécharger le fichier
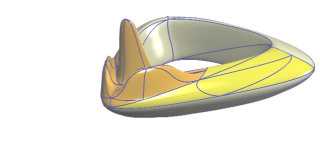 flying3c.jpg (39.38 Ko)
Télécharger le fichier
flying3c.jpg (39.38 Ko)
Télécharger le fichier
 flying4.jpg (33.07 Ko)
Télécharger le fichier
flying4.jpg (33.07 Ko)
Télécharger le fichier
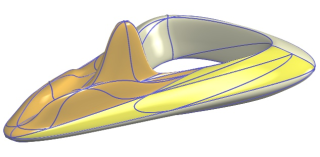 flying4c.jpg (54.96 Ko)
Télécharger le fichier
flying4c.jpg (54.96 Ko)
Télécharger le fichier
 flyingSaucer.jpg (85.11 Ko)
Télécharger le fichier
flyingSaucer.jpg (85.11 Ko)
Télécharger le fichier
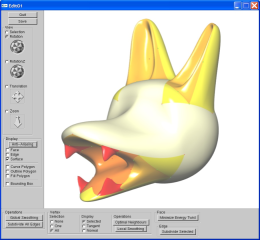 modeler.jpg (146.66 Ko)
Télécharger le fichier
modeler.jpg (146.66 Ko)
Télécharger le fichier
Origine : Fichiers produits par l'(les) auteur(s)
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Format : Figure, Image
Loading...